3. Trigonometry
e. Inverse Trig Functions
1. Inverse Functions (Review)
Before discussing inverse trig functions, we need to understand inverse functions in general. These are covered in the chapter on Functions.
Given a function, \(f\), its inverse function
is a function, \(g\), (if it exists) which undoes the action of \(f\) and
vice versa. Thus:
\(a=g(b)\) if and only if \(b=f(a)\)
Combining these, we get
\(a=g(f(a))\) and \(b=f(g(b))\)
Either of these two equations can also be used to define the inverse function.
The inverse of \(f\) is frequently denoted by \(f^{-1}\). Then the above
equations become:
\(a=f^{-1}(b)\) if and only if \(b=f(a)\)
Combining these, we get
\(a=f^{-1}(f(a))\) and \(b=f(f^{-1}(b))\)
Caution: Don't get confused between the \(-1\) superscript on a function, which denotes an inverse function \(f^{-1}\), and the \(-1\) superscript on a number, which denotes a reciprocal \(5^{-1}=\dfrac{1}{5}\). This is particularly confusing when we talk about trig functions, since we frequently write \(\sin^2(x)\) to mean the square of \(\sin(x)\), but we write \(\sin^{-1}(x)\) to mean the inverse function of \(\sin(x)\) which is NOT the reciprocal \(\dfrac{1}{\sin(x)}\).
Graphs
We plot \(f\) as the graph of the equation \(y=f(x)\) (shown in red) and we plot \(g\) as the graph of the equation \(y=g(x)\) (shown in blue). If \((a,b)\) is on the graph of \(f\), i.e. \(b=f(a)\), then \((b,a)\) is on the graph of \(g\), i.e. \(a=g(b)\). The points \((a,b)\) and \((b,a)\) are related by interchanging the \(x\) and \(y\) components. Geometrically, the points \((a,b)\) and \((b,a)\) are mirror images through the \(45^\circ\) line \(y=x\) (which is simply called the principal diagonal.) Consequently, the graph of the inverse function \(y=g(x)\) is the mirror image of the graph of the function \(y=f(x)\) through the principal diagonal.
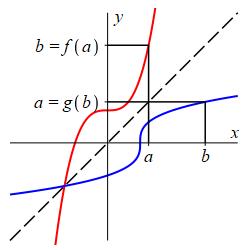
\(g\) must be single valued; so \(f\) must be one-to-one
Every function must be single-valued, i.e. it must satisfy the vertical line test. (Every vertical line hits the graph of \(g\) at most once.) So for the inverse, \(g\), to exist, it must satisfy the vertical line test. Then since \(f\) is the mirror image of \(g\), it must satisfy the horizontal line test. (Every horizontal line hits the graph of \(f\) at most once.) This says \(f\) must be one-to-one. (Every output value of \(f\) occurs at most once.) If \(f\) is not one-to-one, then it cannot be inverted.
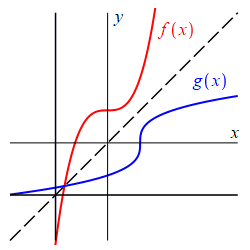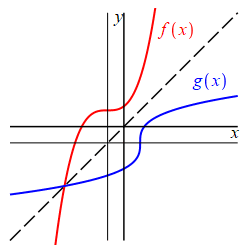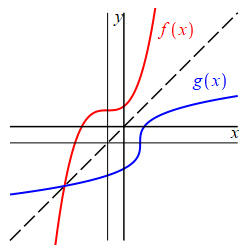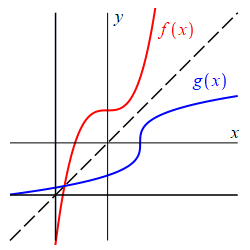
What if \(f\) is not one-to-one?
If \(f\) is not one-to-one, then we pick a piece of the function which is one-to-one and invert that. The piece is called a branch of the function and is obtained by cutting down the domain of \(f\). For example, the function \(f(x)=x^2\) is not one-to-one because \(f(2)=4\) and also \(f(-2)=4\). So we cut down the domain and only consider the branch of the function for \(x \ge 0\). Then \(x^2\) is one-to-one and its inverse is \(g(x)=\sqrt{x}\). (Recall that the radical symbol \(\sqrt{\ \ }\) always gives the positive square root.) This is the standard branch of \(x^2\) for finding an inverse.
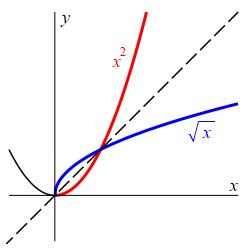
The same thing happens for each of the trig functions. They are not one-to-one since they are periodic. So we pick a standard branch and define the inverse for that branch. This is done on the next three pages.
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum